今月の言葉抄 2006年7月
ピタゴラスの定理が証明できた
今回はまったくの遊び心で自分が書きます。(管理人)
先日、紙と鉛筆で何気なく描いていると、ピタゴラスの定理が証明できた。かなり以前にも一度できたことがあるが、そのあとやってみてもどうしても思い出さなかった。今は中学三年生が、三平方の定理として習うのだそうです。そのころ、数学の授業で何をやっていたか全然記憶にない。
数学に強い人から見れば、ピタゴラスの定理などつまらないことをやっていると思われるだろうが、中学・高校で習ったことを、大人になってもよく覚えている人は意外と少ないものです。例えば英語など六年間習ったでしょうが、まるっきりだめな人がほとんどでしょう。だから何十年も社会人をやって、普段数学などまったく縁のない者が、ある日やってみて突然証明できたことは、喜ばしいことです。老化現象を逆転させたと言えるでしょう、もしかしたら中学三年生のレベルまで。
大人になってピタゴラスの定理に出会う機会はほとんどない。私はたまたま一般向け特殊相対性理論の解説書のなかで、その原理の説明に使われていたのを覚えている。ギリシャ時代に発見された定理が、20世紀の物理学の基本原理の説明に、必要な定理として、使われているのに驚いた記憶がある。
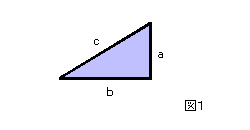
ピタゴラスの定理は「直角三角形の斜辺の二乗は、他の二辺の二乗の和に等しい」というものです。図1で、直角三角形の斜辺を c 他の二辺をそれぞれ a b とすれば、 c² = a² + b²という関係が成り立つというものです。
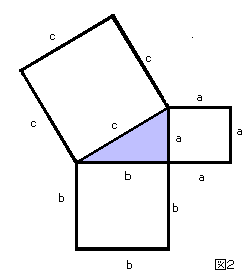
さて、c²も a²も b² も、言い換えれば、それぞれ c a b を辺とした正方形の面積です。それで、図2は c a b を各辺とした正方形を、直角三角形の各辺にそって描いたものです。これが c² = a² + b² を図にしたものですが、これだけでは、 c を辺とした一番大きい正方形と、他の a b を辺とした正方形の和が等しいとは言えません。比べられないのです。いくら見ていても、また移動させても、比べる方法はないようです。
それで別の方法を考えます。
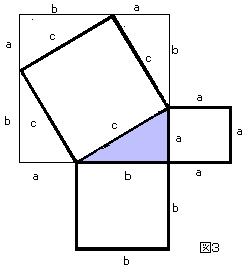
どうすれば証明できるか。ここで、思い付きまたはひらめきが必要になります。論理ではなく、ちょっと飛躍しなければならない。図3は、直角三角形 a の辺を上に垂直に延ばし、さらに左に直角に曲がり、さらに直角に下に下ろして、底辺 b の線と交わるようにし、c を辺とした正方形の角に接線となるように大きな四角形を描いたものです(図中の細い線)。考えるヒントとなる補助線を引いてみたわけです。すると最初の直角三角形の他に、三つの直角三角形ができています。この四つの直角三角形は同じ形をしているように見えますが、本当に同じ形で同じ面積でしょうか。斜辺が c の直角直角三角形は、一意的に他の辺は a b となり、同一です。あるいは他の二辺が a b である直角三角形の斜辺は c でありこれも同一になります。この証明が必要だと思われる方には、このページの最後を読んでください。
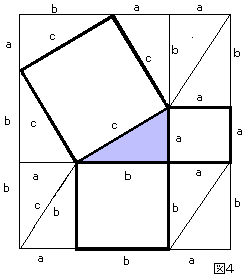
これですぐ証明にかかる人もいますが、まだ a と b の二乗または正方形があります。その補助線も同様に描きますと、図4が出来上がります。これを良く見ると、次のような構成になっているのが分かります。
1)外側は、大きな四角形になっています。この面積はだせます。
2)その内側は、同じ形で同じ面積の直角三角形が最初のも合せて10個あり、c a b を辺とした正方形が3個あります。この面積もだせます。
この二つの面積、1)と2)は等しいでしょう。これを方程式で表します。
1)の面積は、(ヨコ辺)×(タテ辺)で( 2a + b )( a +2b )となります。
2)の面積は、(直角三角形×10個)+( c の正方形)+( b の正方形)+( a の正方形)で、、式で表すと、½ab×10 + c² + a² + b² となります。
これを方程式に書き直すと、
( 2a + b )( a +2b )= ½ab×10 + c² + a² + b²となり、
2a² + 4ab + ab +2b² = 5ab + c² + a² + b²
a²+b²= c² あるいは c²= a²+b² が得られます。これでめでたく証明できました。
古代エジプトでは、3:4:5 の比率の紐は、直角を作ることが知られていたそうです。直角ができなければ、あの大きなピラミッドはできなかったでしょう。これは 5² = 3² + 4² → 25 = 9 + 16 となります。
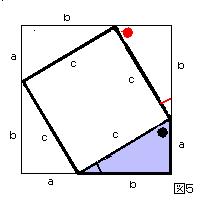
斜辺が c の直角三角形はみな同一です。図5を見てみましょう。この図において、最初の直角三角形の角 / と上の直角三角形 / の角は等しく、同様に●と●の角は等しことを示しています。三角形の内角の和は180°ですし、直線上の角度も180°です。最初の三角形は、直角のほかに / と●の角があります。この二つの角の和は90°です。最初に a から垂直に上に延ばした直線上で、c の正方形の角が直角なので、残りの二つの角/と●の和は90°になります。したがって角/と/は同じ角度です。同様に、●と●も同じ角度です。斜辺 c をもつ直角三角形の他の二つの角が同じであれば、同一の三角形でしょう。したがって四つの直角三角形はすべて同一と言えます。各辺も図に描いたように a と b になります。